![H = H0[N e-,0e+]+ H1[(N + 1)e-,1e+]+ H2[(N + 2)e-,2e+]+ ...](mettec0x.gif)
It is now well accepted that accurate predictions of electronic properties of heavy atoms cannot be achieved without the introduction of relativistic corrections. To include these corrections the relativistic counterpart of the N-electron Schroedinger equation would be an extension of the two particle Salpeter and Bethe [1] equation generalized to include an external field [2]. Unfortunately such an equation suffers from two problems: firstly, it involves an integral kernel that cannot be written in a closed form; and, secondly it depends on more than one time variable and consequently cannot be reduced to a Hamiltonian form. The first of these problems originates from the fact that any relativistic quantum theory conserves only the total charge of the system but not the number of particles. The second problem arises from the requirement of a fully relativistic covariance. Because of these difficulties, almost all practical calculations are done using an effective electron-electron interaction.
The most commonly used approximation is the so called ”no pair” approximation in which the effective Hamiltonian explicitly excludes electron-positron pairs. Thus writing formally the Hamiltonian of a N electron system as
![H = H0[N e-,0e+]+ H1[(N + 1)e-,1e+]+ H2[(N + 2)e-,2e+]+ ...](mettec0x.gif) | (1) |
only the first term of the expansion is taken into account. Then, as in the non relativistic case, we consider a
sum of one-electron and two-electron interactions. Both of these interactions include an expansion in term of
the coupling constant (i.e. the fine structure constant  ). The choice of the Dirac one-electron operator
enables to sum the whole series in powers of
). The choice of the Dirac one-electron operator
enables to sum the whole series in powers of  for the one-electron interaction with the nuclear field
considered as a classical external field (we neglect at this stage field quantization that gives rise to quantum
electrodynamics corrections). The electron-electron interaction must obviously be deduced from quantum
electrodynamics (QED). This is generally achieved in the bound state picture of the S-matrix with the result
that, after time integration, the interaction reduces to a generalized form of the Breit operator
[3].
for the one-electron interaction with the nuclear field
considered as a classical external field (we neglect at this stage field quantization that gives rise to quantum
electrodynamics corrections). The electron-electron interaction must obviously be deduced from quantum
electrodynamics (QED). This is generally achieved in the bound state picture of the S-matrix with the result
that, after time integration, the interaction reduces to a generalized form of the Breit operator
[3].
Following the approach outlined above, a computer code has been written to handle relativistic calculations for atoms. The present version is an update of the code first published in 1975 [4]. This version make use of the multiconfiguration approximation for the N electron wavefunction. In this scheme both one-electron orbitals and mixing coefficients between the various configurations are fully optimised during a double step self consistent process. In the first step, the mixing coefficients between the configurations are kept fixed while the radial equations are solved self-consistently. The second step optimises the mixing coefficients between the configurations through a diagonalization of the Hamiltonian matrix.
This chapter is organised as follows: the first section presents a short summary of the multiconfiguration Dirac-Fock method (MCDF). Section 2 describes the reduction of the expectation value of the Hamiltonian to radial integrals. Section 3 is devoted to the numerical solution of the self consistent integro-differential equations. The radiative corrections are surveyed in section 4 and the last section provides a short description of the options available in the package.
As in many self-consistent field method, the starting point to build up N-electron wavefunctions are central field one-electron orbitals, thus in the relativistic case use is made of the Dirac four component spinors:
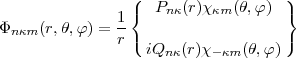 | (2) |
these spinors are simultaneous eigenfunctions of the parity operator, the square of the total angular
momentum operator j = l + s and of its z-component. The quantum numbers n, ,m are respectively the
principal quantum, the relativistic ”kappa” quantum number that includes both the parity and the total
angular momentum j and m is the eigenvalue of jz. The quantum number j,
,m are respectively the
principal quantum, the relativistic ”kappa” quantum number that includes both the parity and the total
angular momentum j and m is the eigenvalue of jz. The quantum number j, ,l are related through:
,l are related through:
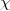
 m in Eq.(2) are the two component Pauli spherical spinors:
m in Eq.(2) are the two component Pauli spherical spinors:
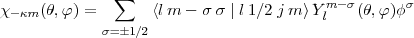 | (4) |
where the terms under the summation are respectively a Clebsch-Gordan coefficient, a spherical harmonic and one of the two Pauli spinors:
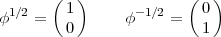 | (5) |
The Dirac spinors as defined by Eq.(2) are used to build Configuration State Functions (CSF)
| 
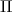 JM > that are antisymmetric products of the one-electron wavefunctions and are eigenvalues of
the parity
JM > that are antisymmetric products of the one-electron wavefunctions and are eigenvalues of
the parity 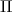 , the total angular momentum J and its projection M. The label
, the total angular momentum J and its projection M. The label  stands for all
other values (angular momentum recoupling scheme, seniority numbers, ...) necessary to define
unambiguously the CSF. For a N-electron system, a CSF is thus a linear combination of Slater
determinants:
stands for all
other values (angular momentum recoupling scheme, seniority numbers, ...) necessary to define
unambiguously the CSF. For a N-electron system, a CSF is thus a linear combination of Slater
determinants:
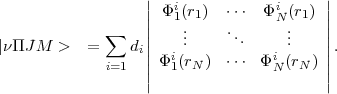 | (6) |
all of them with the same 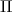 and M values while the di’s are determined by the requirement that
the CSF is an eigenstate of J2. The method used in the package to build these eigenstates is
described in Appendix A. The total MCDF wavefunction is constructed as a superposition of CSF’s,
i.e.
and M values while the di’s are determined by the requirement that
the CSF is an eigenstate of J2. The method used in the package to build these eigenstates is
described in Appendix A. The total MCDF wavefunction is constructed as a superposition of CSF’s,
i.e.
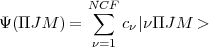 | (7) |
As pointed out in the introduction, the relativistic effective Hamiltonian for an N-electron atomic system is taken as the Dirac Breit Hamiltonian given by:
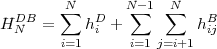 | (8) |
with for the Dirac operator
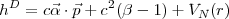 | (9) |
here and throughout this chapter we make use of atomic units. Thus e = h/2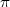 = me = 1 and c = 1/
= me = 1 and c = 1/ where e
is the absolute value of the electron charge, h the Plank constant, me the mass of the electron, c the speed of
light and
where e
is the absolute value of the electron charge, h the Plank constant, me the mass of the electron, c the speed of
light and 
 1/137 the fine structure constant. The 4x4 Dirac matrices
1/137 the fine structure constant. The 4x4 Dirac matrices  i and
i and 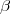 are given
by
are given
by
 | (10) |
in terms of the 2x2 Pauli matrices  i and the 2x2 zero and unit matrix I. V N(r) is the nuclear potential. For
the electron-electron interaction the Breit operator
i and the 2x2 zero and unit matrix I. V N(r) is the nuclear potential. For
the electron-electron interaction the Breit operator
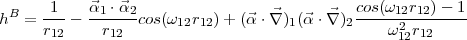 | (11) |
includes the instantaneous Coulomb repulsion, the magnetic interaction and the retardation in the
electron-electron interaction due to the finite value of the speed of light. 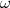 12 is the frequency of the exchange
photon and, in an independent model description is given by
12 is the frequency of the exchange
photon and, in an independent model description is given by 
 , the
, the  ’s being the electron binding
energies. At this point it is worth to point out that:
’s being the electron binding
energies. At this point it is worth to point out that:
- the electron-electron interaction is expressed in the Coulomb gauge and this the correct one to
use as long as a finite summation (in terms of the number of photon lines) is included in the
framework of the Dirac-Fock potential. As pointed out first by Love [5] and more recently studied by
Sucher [6] and Lindgren [7] the use of another gauge, like the Lorentz one, will introduce at
each order of the perturbation series a spurious contribution that will be cancelled at the next
order of the expansion. Obviously this gauge dependence arises only from the approximation
inherent to any practical calculation and furthermore is specific to the approximation used. For
example when a local potential is used to define the single particle states, the result is gauge
independent [8]. This gauge problem is indeed the same as the one, well known in non relativistic
calculations, that occurs when computing dipole transitions in the so-called length and velocity
forms.
- the retardation part beyond the zero frequency limit (i.e. the limit obtained by setting 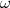 12 = 0 in Eq.(11))
can only be used at the Dirac-Fock level since Koopman’s theorem can be used to obtain an approximation of
the binding energies. On the other hand as soon as more than one configuration is included, the MCDF
method does not provided any easy way to get approximated one-particle energies. This is an example of one
yet unsolved problem in the framework of the multiconfiguration approach to relativistic correlation
energies.
12 = 0 in Eq.(11))
can only be used at the Dirac-Fock level since Koopman’s theorem can be used to obtain an approximation of
the binding energies. On the other hand as soon as more than one configuration is included, the MCDF
method does not provided any easy way to get approximated one-particle energies. This is an example of one
yet unsolved problem in the framework of the multiconfiguration approach to relativistic correlation
energies.
- the Hamiltonian as given in Eq.(8) is the so-called ”no-pair” approximation in the sense that it excludes
explicitly any contribution from electron-positron pairs. Consequently care as to be taken to avoid
contribution from the negative continuum. As no projection operators are included in the present version of
the package, problems of convergence may show up for large values of the nuclear charge and/or correlated
orbitals of high principal quantum numbers [9]. An updated version of the program (under development) will
try to take care of this problem.
From what has been discussed in the previous section, the expectation value of the total Hamiltonian will
include contributions from:
- the one particle Dirac Hamiltonian
- the Coulomb repulsion
- the Breit interaction
that, using A,B,C,... as label for the one electron orbitals, can be written respectively as
![< > [ integral
A |hD |B = dkA,kBdmA,mB - -22 [QAQB] dr +
1 integral a[ (dPA-- kA- ) (dQA-- kA- )]
a integral QB dr + r PA - PB dr - r QA dr +
[(PAPB + QAQB) VN ]dr ]](mettec12x.gif) | (12) |
where the three radial integrals are respectively the contributions of substracting the rest mass energy, the
kinematic operator 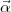 .
.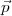 and the nucleus-electron interaction.
and the nucleus-electron interaction.
For the instantaneous Coulomb repulsion, the usual multipole expansion of 1/r12 leads to:
![< AB |r1-|CD > = dmA+mB,mC+mD sum k dk(jC mC ,jAmA)dk(jBmB, jDmD)
12 integral integral [P (1)P (1) + Q (1)Q (1)]U (1,2)[P (2)P (2)+ Q (2)Q (2)]dr dr
A C A C k B D B D 1 2](mettec15x.gif) | (13) |
where Uk(1,2) = 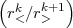 , r< being the smaller of (r1,r2) and r> the larger. The dk’s are angular
coefficients given, in terms of Wigner 3j symbols, by:
, r< being the smaller of (r1,r2) and r> the larger. The dk’s are angular
coefficients given, in terms of Wigner 3j symbols, by:
![( ) ( )
dk(jm, j'm') = (- 1)m'+12 [(2j + 1)(2j'+ 1)]1/2 j k j' j k j'
12 0 - 12 - m mk m'](mettec17x.gif) | (14) |
for which the following triangular conditions must hold:
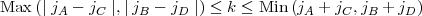 | (15) |
while lA + lC + k and lB + lD + k must both be even.
As given in Eq.(11) the Breit interaction includes the two contributions:
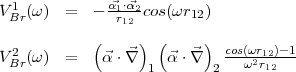 | (16) |
The reduction to radial integrals gives for the first term V Br1(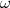 ):
):
![sum
< AB |VB1r(w) |CD >= dmA -mC,mB -mD L,k(- 1)L+k+jC+jD- mC- mAdL(jAmA, jC mC )dL(jBmB, jDmD)
[ L L k L L k
- zk (A,C)z k (B,D)R M(AC, BD) + zk (A,C)z k (B,D)R M(AC, BD)
]
+zLk (A, C)zLk (B, D)RkM (CA, BD) - zLk (A, C)zLk (B, D)RkM (CA, BD)](mettec20x.gif) | (17) |
with the triangular conditions:
while lA +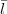 C + k and lB +
C + k and lB + 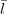 D + k must both be even. The dL coefficients are those given by Eq.(14) and the
D + k must both be even. The dL coefficients are those given by Eq.(14) and the 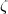 coefficients are defined as:
coefficients are defined as:
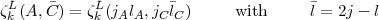 | (19) |
thus 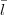 is the orbital quantum number for the small component. At this stage it is also worth to remember
that
is the orbital quantum number for the small component. At this stage it is also worth to remember
that  small = -
small = - large. Furthermore
large. Furthermore
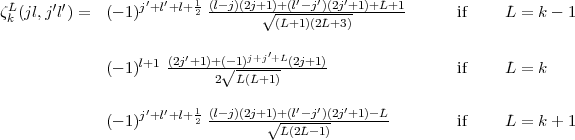 | (20) |
The radial integral itself is given by
![integral integral
RkM(AC, BD) = - w(2k + 1) [PA(1)QC (1)jk(wr<)jk(wr >)PB(2)QD(2)] dr1dr2](mettec27x.gif) | (21) |
jk and 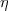 k are the regular and irregular spherical Bessel functions.
k are the regular and irregular spherical Bessel functions.
The second term V Br2(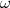 ) of the Breit operator reduces to:
) of the Breit operator reduces to:
![sum
< AB |VB2r(w) |CD > = dmA -mC,mB -mD (- 1)jC+jD-mC -mA L dL(jAmA, jCmC )dL(jBmB, jDmD)
sum ( L 1 k ) ( L 1 k )
k1,k2 (2k1+(21L)(+21k)2+1)- 1 2
[ 0 0 0 0 0 0
- zLk1(A, C)zLk2(B,D)RLkR1k2 (AC, BD) + zLk1(A,C)zLk2(B, D)RLkR1k2 (AC, BD)
+zL (A, C)zL (B,D)RLk1k2 (CA, BD) - zL (A, C)zL (B,D)RLk1k2 (CA, BD)]
k1 k2 R k1 k2 R](mettec28x.gif) | (22) |
with the same triangular and parity conditions as for the B1 integrals. The radial integrals are here defined as:
![integral integral
RLkR1k2(AC, BD) = [PA(1)QC (1)WL,k1,k2(1,2)PB(2)QD(2)] dr1dr2](mettec29x.gif) | (23) |
with
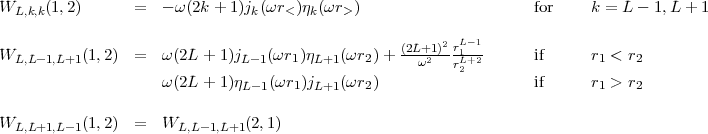 | (24) |
When 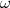 = 0 the two terms of Eq.(16) reduce to
= 0 the two terms of Eq.(16) reduce to
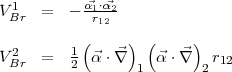 | (25) |
Using the expansions for the Bessel fonctions
![--zn--[ z2/2 --(z2/2)2--- ]
jn(z) = (2n+1)!! 1 - 2n+3 + 2(2n+3)(2n+5) ...
[ ]
jn(z) = (2n-1)!! 1 - z2/2+ --(z2/2)2---...
zn+1 2n-1 2(2n-1)(2n-3)](mettec32x.gif) | (26) |
the radial integral of Eq.(21) reduces to:
![integral integral
RkM(AC, BD) = [PA(1)QC (1)Uk(1,2)PB(2)QD(2)] dr1dr2](mettec33x.gif) | (27) |
and the definition of the radial operator W simplifies to:
![WL,k,k(1,2) = (2L+1)-Uk(1,2) for k = L - 1,L + 1
(2k+1)
(2L+1)
WL,L -1,L+1(1, 2) = --2---[UL+1(1, 2)- UL -1(1,2)] if r1 < r2
0 if r1 > r2
WL,L+1,L -1(1,2) = WL,L- 1,L+1(2,1)](mettec34x.gif) | (28) |
As in the non-relativistic case, it is useful to introduce the concept of the average energy defined as the centre of gravity of all the levels belonging to a given (jj) configuration and given by
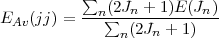 | (29) |
The usefulness of the average energy is due to the fact that the energy of a given level is just the sum of EAv plus a small number of extra two electron integrals. As the expression of EAv is very easy to incorporate in any computer code, this make the input data for a given level rather convenient to specify. The average energy is most easily obtain from the interaction of a single electron with a closed shell. Using the well known closure properties of the Wigner 3j symbols:
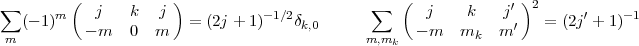 | (30) |
we obtain for the coefficients of the diract Coulomb integrals
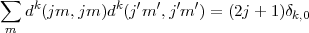 | (31) |
and for the exchange Coulomb integrals:
![sum [ ] ( ' )2
dk(jm, j'm') 2 = (2j + 1)Gjkj' with Gjkj'= j k j
m 1/2 0 - 1/2](mettec38x.gif) | (32) |
For the first contribution to the Breit operator, the triangular relations of Eq.(18) combined with the result of Eq.(31) show that there is no contribution from direct integrals as expected since a closed shell has a zero net magnetic moment. For the exchange integrals we obtain:
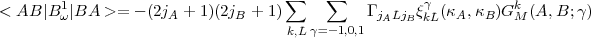 | (33) |
where, using the definition of Eq.(27) for the radial integrals, we have defined:
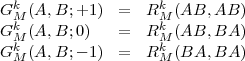 | (34) |
and
![q±1 (kA,kB) = (kA-kB+k)2 q0 (kA,kB) = 2[(kA-kB)2-k2]
k,k-1 k(2k+1) k,k-1 k(2k+1)
(k +k )2
q±k1,k(kA,kB) = --Ak(k+B1)- q0k,k-1(kA,kB) = 2q±k1,k
±1 (kA-kB--k-1)2 0 2[(kA-kB)2-(k+1)2]
qk,k+1(kA,kB) = (k+1)(2k+1) qk,k+1(kA,kB) = (k+1)(2k+1)](mettec41x.gif) | (35) |
With the help of the above relations we can now write the explicit expression of the average energy that, restricted to Coulomb interaction for simplicit, reads:
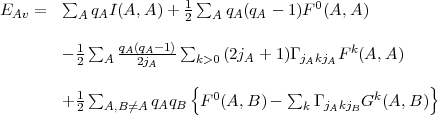 | (36) |
the q’s are the occupation numbers of the orbitals and the one-electron integrals I are those defined by Eq.(12). The direct Coulomb integrals Fk are the radial integrals of Eq.(13) in which C = A and D = B while the exchange integrals Gk are obtained from the same equation by setting C = B and D = A.
For simplicity we use only orthonormalized Dirac spinors according to:
![integral
[PA(r)PB(r) + QA(r)QB(r)] dr = dk ,k dn ,n
A B A B](mettec43x.gif) | (37) |
Then the MCDF equations are obtained by writing E = 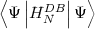 /
/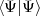 and using a variational
principle on both the c
and using a variational
principle on both the c coefficients, and on the large and small radial components Pn
coefficients, and on the large and small radial components Pn (r) and Qn
(r) and Qn (r).
Variation of the c
(r).
Variation of the c leads to a Hamiltonian matrix from which the c
leads to a Hamiltonian matrix from which the c are deduced by diagonalization.
Variation with respect to the radial wavefunctions leads to an integro-differential equation that for a given
orbital A reads:
are deduced by diagonalization.
Variation with respect to the radial wavefunctions leads to an integro-differential equation that for a given
orbital A reads:
) sum ( QB(r) ) ( XQ (r) )
d-raV (rr) ad-- kA- Q (r) = a eA,B - P (r) + - X A (r)
A dr r A B B PA](mettec46x.gif) | (38) |
where V A is the sum of the nuclear potential and the direct Coulomb potential while XPA and XQA include
all the two-electron interactions excepted for the direct Coulomb instantaneous repulsion.  A,B are Lagrange
parameters used to enforce the orthogonality constraints of Eq.(37) and thus the summation over B run only
for orbitals with
A,B are Lagrange
parameters used to enforce the orthogonality constraints of Eq.(37) and thus the summation over B run only
for orbitals with  B =
B =  A.
A.
Most of the numerical methods used to solve the relativistic Hartree-Fock equations are drawn from what has been known for a long time in the non relativistic case (see [10]). The integro-differential equations are solved by an iterative process that reduces, at each step, the integro-differential equations to simple differential equations by considering the potential terms (direct and exchange) as given source functions computed from the wave function obtained from the previous step. The iterative process is then continued until a given accuracy is reached between two successive iterations. Obviously the need to solve a pair of two first order coupled differential equations instead of a single second order differential equation will introduce some modifications in the recipes available since the pioneer work of Hartree [11].
These methods are based on the following strategy: to obtain the function at the mesh point n+1 use is made of the known values at the preceding N points to predict a first estimate, this estimate is inserted in the differential equation to obtain the derivative that in turn is used to correct the first estimate, then the final value may be taken as a linear combination of the predicted and corrected values to increase the accuracy. As an example we consider the five points Adams’ method that has been widely selected because of its stability properties [12]. The predicted, corrected and final values are given respectively by:
where p' and y' stand for the derivatives with respect to the tabulation variable. The linear combination for the final value is defined as to cancel the term of order h6, h being the constant interval step of the mesh. In the above equations y stands for either the large P or small Q radial wave function. As in the non relativistic case, the solution involves both an inward and an outward integration for stability purposes. The outward integration is started by means of power series near the nucleus to provide the first five points needed to start the Adams’ scheme. For the inward integration a far enough point is selected empirically such that the wave function are assumed to have reached their asymptotic exponential decay, this asymptotic behaviour provides the five starting points. The drawback of this method is, because neither the slopes at origin nor at infinity are known in advance, that for arbitrary values of these slopes neither of the two radial components is continuous at the matching point R. In order to obtain a solution continuous everywhere it is possible to proceed in the following way: first remember that the solution of an inhomogeneous differential equation can be written as the sum of a particular solution of the inhomogeneous equation and of the solution of the associated homogeneous equation (in the present case the equation obtained by neglecting the exchange potentials). Thus if Po and Pi are respectively the outward and inward solutions for the large component, we obtain, with the same labels for the small component: where the subscripts I and H stands for the inhomogeneous and homogeneous solutions. Obviously this continuous solution will not be normalized for an arbitrary value of the diagonal parameter A,A
of Eq.(38). The default in the norm is then used to modify
A,A
of Eq.(38). The default in the norm is then used to modify  A,A until the proper eigenvalue is
found.
A,A until the proper eigenvalue is
found.
As seen in the previous section, the predictor corrector methods require to solve two systems of equations (the homogeneous and inhomogeneous ones) to obtain a continuous solution while in the non relativistic case the Numerov method associated with tail correction [10] provides directly a continuous approximation (the derivative remains discontinuous until the eigenvalue is found). We consider now alternative methods that easily allow to enforce the continuity of one of the two radial components. Let us define the solution at point n+1 as:
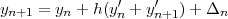 | (41) |
where 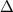 n is a difference correction given, in terms of central differences, by:
n is a difference correction given, in terms of central differences, by:
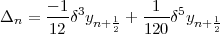 | (42) |
with:
at this stage we may remember that the accuracy of the solution is required only when self consistency is reached. Consequently, the difference correction n can be obtained at each iteration from the wave functions
of the previous iteration as it is done for the potential terms and in so doing we can designed efficient
schemes with respect to computer time. Let:
n can be obtained at each iteration from the wave functions
of the previous iteration as it is done for the potential terms and in so doing we can designed efficient
schemes with respect to computer time. Let:
![r' [ Q ]
an = 1+ kh2 rnn un = DPn + h2[r'nXQn + r'n+1X n+1]
b = -1 + khr'n v = DP + h r'XP + r' XP
n h 2rn ' n h n' 2 n n n+1 n+1
fn = a2 [en - Vn]rn hn = a-rn + hn](mettec52x.gif) | (44) |
where r' stands for dr/dt (to take into account the fact that the tabulation variable t may be a function of r)
and XP(Q) = XPA(QA) +  B
B A
A A,BPB(QB). Furthermore, all the functions of r are calculated, as already
said, with the help of the of the wavefunctions obtained at the previous iteration. Then the system of
algebraic equations:
A,BPB(QB). Furthermore, all the functions of r are calculated, as already
said, with the help of the of the wavefunctions obtained at the previous iteration. Then the system of
algebraic equations:
![[M ]](mettec55x.gif) (PQ) = (uv) with the matrix M given by:
(PQ) = (uv) with the matrix M given by:
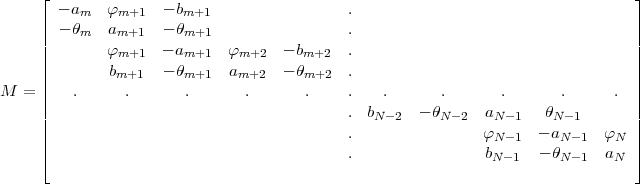 | (46) |
and the two column vectors (PQ) and (uv) defined as:
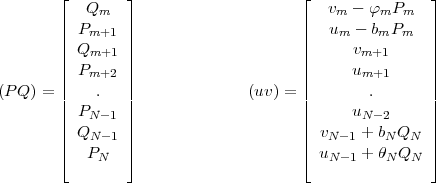 | (47) |
as displays in Eq.(46) each row of the matrix M has at most four non zero elements. To solve this system of
equation the matrix M is decomposed into the product of two triangular matrices M = L.T in which L is a
lower matrix with only three non zero elements on each row and T an upper matrix with the same property.
Introducing an intermediate vector (pq) it is possible to solve L(pq) = (uv) for m, m+1, .., N and then
T(PQ) = (pq) for N, N-1, ..,m. The last point of tabulation N is determined by the requirement that PN
should be lower than a specified small value when assuming QN = 0. Thus the number of tabulation points of
each orbital is determined automatically during the self consistency process. This elimination process
produces, as written here, a large component P that is continuous everywhere. The discontinuity
of the small component at the matching point rm can then be used to adjust the eigenvalue
 A,A.
A,A.
Because the bound orbitals exhibit a rapid variation near the origin and an exponential decay at large values of r it is more efficient to make the change of variable:
 | (48) |
to tabulate all the radial functions on this grid of points equally spaced with respect to this new variable t. The simple logarithmic distribution of the tabulation points is well adapted for not too high principal quantum numbers n (typically for all occupied orbitals throughout the periodic table) but will not give enough points for high n Rydberg orbitals. For this reason we have choosen the second form that is also convenient for continuum orbitals.
As we have to solve the Dirac-Fock radial equations for different purposes (to get initial starting wavefunctions, during the self-consistent multiconfiguration process or to obtain hydrogenic solutions for QED corrections, see section 5) we have implemented two solvers. The first one is designed for homogeneous equations and used the predictor corrector method described in section 4.2.1. Indeed, for the homogeneous equation, it is always possible to get one the two radial functions continuous while the discontinuity in the other one is used to adjust the eigenvalue. For example if the large component P is made continuous, then the first order correction to the eigenvalue is given by:
![[ - + ] integral oo [ 2 2 ]
de = cP(R) Q(R )- Q(R ) P (u) + Q (u) du
0](mettec59x.gif) | (49) |
where R is the matching point for the inward and outward integrations. This method has the advantage to be both fast and rather accurate.
As described in section 4.2.2 the finite difference method is well adapted for Dirac-Fock orbitals but less for correlation ones. Indeed it is rather difficult to obtain a good estimate of these correlation orbitals and the rather poor intrinsic accuracy of the finite difference method may result in instabilities during the self consistent field process. We thus proceed in the following way: the outward integration is performed using the predictor corrector method while the outward integration uses the finite difference method to insurance continuity of the large component. But to increase the accuracy an extra loop is introduced in the inward integration scheme in order to compute the central differences of Eq.(43) from the wave function being solved.
Calculation of many-electron radiative corrections is still one the most difficult numerical problem to deal
with for high-precision level predictions. Even if recent progresses have been achieved [13, 14, 15], it is rather
difficult to include them as standard procedures in distributed computer codes. Nevertheless as, at least an
estimation of the order of magnitude of these corrections, has to be included in present days
relativistic calculations, we have provided some estimations for them. These corrections include two
contributions:
1) the vacuum polarization, for which effective potentials can be deduced from Quantum Electro-Dynamics
(QED)
2) the self-energy, the first-order contribution of which is known exactly (i.e. to all orders in the external field
strength Z ) for hydrogen-like systems [16, 17, 18]
) for hydrogen-like systems [16, 17, 18]
This contribution is related to the creation and annihilation of virtual electron-positron pairs in the field
of the nucleus. The first term of order  (Z
(Z ) with respect to the nuclear Coulomb potential
can be evaluated, following Wichmann and Kroll [19], as the expectation value of the Uehling
potential [20]. In the case of a nuclear spherical charge distribution
) with respect to the nuclear Coulomb potential
can be evaluated, following Wichmann and Kroll [19], as the expectation value of the Uehling
potential [20]. In the case of a nuclear spherical charge distribution 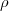 N(r) this potential is given
by:
N(r) this potential is given
by:
![integral oo [ ( ) ( )]
U(r) = - 2ace- urN(u) K0 ----2--- - K0 ---2---- du
3r 0 ce|r- u | ce|r + u|](mettec60x.gif) | (50) |
where 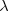 e is the Compton wavelength of the electron and the function K0(x) is defined as:
e is the Compton wavelength of the electron and the function K0(x) is defined as:
![integral [ ]
K (x) = oo t-3 + (2t)-5 (t2- 1)1/2e- xtdt
0 1](mettec61x.gif) | (51) |
Terms of higher order can also be evaluated as the expectation value of potentials. The correction of order
 2(Z
2(Z ) is associated to the Kallen and Sabry [21] potential while the term of order
) is associated to the Kallen and Sabry [21] potential while the term of order  (Z
(Z )3 has been
given by Blomqvist [22]. Various analytical approximations [23, 24] are available to calculate the
various functions like K0 in Eq.(51) involved in the vacuum polarization potentials of various
orders.
)3 has been
given by Blomqvist [22]. Various analytical approximations [23, 24] are available to calculate the
various functions like K0 in Eq.(51) involved in the vacuum polarization potentials of various
orders.
The contribution of the other bound electrons to the vacuum polarization can be estimated in
analogy with that of the nucleus by replacing 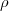 N(r) in Eq.(50) by the electronic charge of the
electrons.
N(r) in Eq.(50) by the electronic charge of the
electrons.
This second contribution arises from the interaction of the electron with its own radiation field. For one-electron systems this self self-energy term has been calculated exactly by P.J. Mohr [25, 17, 18] and expressed as:
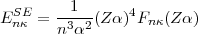 | (52) |
where F(Z ) is a slowly varying function of Z
) is a slowly varying function of Z . Previous approximations of the self-energy in many-electron
atoms used an effective Z value to scale the above hydrogenic results, the effective Z being deduced from the
comparison of the mean value of the radius of the Dirac-Fock orbital with that of the hydrogenic
one. It has been shown [26] that this effective Z approximation may be completly wrong for
excited states and must be replaced by a more physical prescription to obtain the effective Z. This
prescription is based upon the Welton picture of the Lamb-shift [27] in which the self-energy is
due to the perturbations induced in the electron classical trajectory by the fluctutation of the
electromagnetic field of the vacuum. Driven by these flucuations, the electron explores the field of the
nucleus over a region of extension
. Previous approximations of the self-energy in many-electron
atoms used an effective Z value to scale the above hydrogenic results, the effective Z being deduced from the
comparison of the mean value of the radius of the Dirac-Fock orbital with that of the hydrogenic
one. It has been shown [26] that this effective Z approximation may be completly wrong for
excited states and must be replaced by a more physical prescription to obtain the effective Z. This
prescription is based upon the Welton picture of the Lamb-shift [27] in which the self-energy is
due to the perturbations induced in the electron classical trajectory by the fluctutation of the
electromagnetic field of the vacuum. Driven by these flucuations, the electron explores the field of the
nucleus over a region of extension 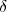 r, its trajectory being defined by r. The electron then probes a
potential V N(r +
r, its trajectory being defined by r. The electron then probes a
potential V N(r + 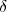 r) instead of the unperturbed potential V N(r). The perturbation potential then
reads:
r) instead of the unperturbed potential V N(r). The perturbation potential then
reads:
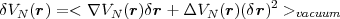 | (53) |
as the mean value of fields in the vacuum are zero, < 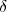 r >= 0 and the perturbation reduces
to:
r >= 0 and the perturbation reduces
to:
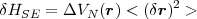 | (54) |
In this picture < (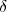 r)2 > is infinite and must be renormalized. Taking advantage that exact hydrogenic
results are available, the screened self energy correction for s orbitals can be obtained from the following
relation:
r)2 > is infinite and must be renormalized. Taking advantage that exact hydrogenic
results are available, the screened self energy correction for s orbitals can be obtained from the following
relation:
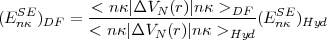 | (55) |
where the subscripts DF and Hyd stand for the Dirac-Fock and Hydrogenic Dirac orbitals. If a finite nuclear size is used, this method automatically includes the volume effect in the self energy. For non s orbitals, the main contribution to the self energy is due to the anomalous gyromagnetic ratio of the electron because the electronic density near the nucleus is much smaller than for s orbitals.
We illustrate in the two following tables the respective accuracy of the various approximations to the
screening of the self-energy. In the low Z region, the Kabir and Salpeter equation [28] provides a good
approximation since relativistic corrections to the radial wavefunctions are small. This equation has been
used by De Serio et al. [29] for various nl,n'l' levels of helium-like ions.
Table I: Self-energy screening contribution (in eV) to the 3PJ  3S1 transitions of helium-like ions.
3S1 transitions of helium-like ions.
| 3P0 -3S1 | 3P2 -3S1 | |||||
| Z | Zeff | Welton | DeSerio(a) | Zeff | Welton | DeSerio(a) |
| 12 | 0.0007 | 0.0046 | 0.0048 | 0.0002 | 0.0040 | 0.0034 |
| 18 | 0.0016 | 0.0105 | 0.0116 | 0.0001 | 0.0089 | 0.0077 |
| 26 | 0.0038 | 0.0258 | 0.0317 | 0.0001 | 0.0216 | 0.0203 |
(a) Ref. [29]
The comparison, given in the above table, of the self-energy contribution to the energy splittings between the 3PJ ans 3S1 levels illustrates the poor performance of the effective Z method to correct for the screening. At high Z nuclear charges, accurate results have been recently obtained by Blundell [15] for lithium-like uranium and the next table show the comparison between his accurate values and the previous semi-empirical or phenomenological estimates of the screening corrections.
Table II: Screening correction (in eV) to the self-energy in lithium-like Uranium
| Orbital | Zeff | Welton | Blundell(a) |
| 2s1/2 | 3.71 | 2.88 | 2.75(2) |
| 2p1/2 | 1.21 | 0.84 | 0.97(2) |
(a) Ref. [15]
The purpose of this section is not to provide a write up for the package but only to outline some specific options of the code. Besides the fact that, after self consistency has been achieved, radiative corrections are added as a first order correction to the total energy, various options are made available for both the nuclear model and the optimisation of the one-electron wavefunctions.
For the inner shell of heavy atoms and more generally for all their s orbitals, it is mandatory to go beyond the point nucleus approximation. For that purpose it is possible to use two nuclear models. The first one assumes that the nuclear charge distribution can be approximated by a uniform charge sphere of radius Rnuc, thus for an atom of atomic number Z the nuclear potential is given by:
![---Z-[ -r2-]
2Rnuc 3 - R2nuc if r < Rnuc
Vnuc(r) =
-rZ if r > Rnuc](mettec66x.gif) | (56) |
A more realistic description of the proton charge distribution inside the nucleus is provided by the Fermi distribution:
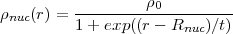 | (57) |
where t is the thickness parameter of the Fermi distribution and 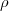 0 is a normalisation constant such that the
integral of the proton charge equals Z. As the detailed proton charge distribution becomes a critical
parameter only for very heavy atoms, the default option of the program is to use an uniformed
charged sphere for atomic numbers lower then 45 and a Fermi distribution with a thickness
parameter t = 2.3 otherwise. Furthermore the code include a table of nuclear radii as given by W.R.
Johnson and G. Soff [30]. This standard option can be overwritten by providing specific nuclear
parameters for the atom under consideration. As an illustration of the influence of the finite
nuclear size, we give in Table III the values of this correction for the low lying hydrogenic energy
levels.
0 is a normalisation constant such that the
integral of the proton charge equals Z. As the detailed proton charge distribution becomes a critical
parameter only for very heavy atoms, the default option of the program is to use an uniformed
charged sphere for atomic numbers lower then 45 and a Fermi distribution with a thickness
parameter t = 2.3 otherwise. Furthermore the code include a table of nuclear radii as given by W.R.
Johnson and G. Soff [30]. This standard option can be overwritten by providing specific nuclear
parameters for the atom under consideration. As an illustration of the influence of the finite
nuclear size, we give in Table III the values of this correction for the low lying hydrogenic energy
levels.
Table III: Finite nuclear size correction (in eV) for hydrogenic levels.
Numbers in parentheses are power of 10
| Z | 1s | 2s | 2p1/2 | 2p3/2 |
| 25 | 0.0436 | 0.0056 | 4.(-5) | 0. |
| 50 | 1.9580 | 0.2556 | 0.0075 | 0. |
| 75 | 42.399 | 5.3110 | 0.3634 | 0. |
| 100 | 451.23 | 92.965 | 13.922 | 6.(-5) |
Two options are available to achieve self consistency. For the first one, both the mixing coefficients between the (jj) configurations and the radial orbitals are fully optimised and such a calculation is what is called MCDF. In the second option only the radial orbitals are optimised while the weights of the configurations are kept fixed. When the weights are frozen, an useful concept to introduce (and included in the code) is the definition of an extended average energy (EAL). This concept introduce almost simultaneously by various authors [31, 32] has the property than the EAL exactly reduces to the non relativistic average energy. The EAL is defined as the sum of the (jj) average energy defined in Eq. (29), sum that includes all the (jj) subconfigurations arising from a single (LS) configuration. In the sum, each of the (jj) subconfiguration is weighted by its degeneracy. As an example, consider the p2 configuration that, in the relativistic case, splits into the three subconfigurations : p1/22, p1/2p3/2, p3/22. The EAL is then defined as:
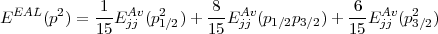 | (58) |
Whatever is the choice selected (MCDF or EAL) for the self consistent process, it is possible to include
either only the instantaneous Coulomb repulsion or both this repulsion and the zero frequency
limit of the first term of the Breit interaction as given by Eq. (25) also known as the Gaunt
interaction. In fact there is no fundamental reason to include only the first term of the Breit
interaction since both term have the same  Z dependence. On the other hand the numerical
value of this first term is typically one order of magnitude larger than the second one given in
Eq. (25). In so doing one save computer time and still get the main contribution of the Breit
interaction to the wavefunctions. Table IV illustrates the changes in the radial wavefunctions of
uranium Beryllium-like when the Gaunt interaction is introduced in the self consistent field
process.
Z dependence. On the other hand the numerical
value of this first term is typically one order of magnitude larger than the second one given in
Eq. (25). In so doing one save computer time and still get the main contribution of the Breit
interaction to the wavefunctions. Table IV illustrates the changes in the radial wavefunctions of
uranium Beryllium-like when the Gaunt interaction is introduced in the self consistent field
process.
Table IV: Change in the radial expectation values < rn > due to the Gaunt interaction (uranium
Beryllium-like). The calculation includes the two 1s22s2 and 1s22p2 configurations.
Numbers in parentheses are power of 10.
| 1s | 2s | 2p1/2 | 2p3/2 | ||
| < r-3 > | (a) | n.a. | n.a. | n.a. | 3.404(4) |
| (b) | n.a. | n.a. | n.a. | 3.582(4) | |
| < r-1 > | (a) | 1.230(2) | 3.205(1) | 3.187(1) | 2.349(1) |
| (b) | 1.227(2) | 3.202(1) | 3.175(1) | 2.374(1) | |
| < r > | (a) | 1.356(-2) | 5.455(-2) | 4.406(-2) | 5.226(-2) |
| (b) | 1.359(-2) | 5.462(-2) | 4.419(-2) | 5.185(-2) | |
| < r2 > | (a) | 2.576(-4) | 3.580(-3) | 2.441(-3) | 3.220(-3) |
| (b) | 2.587(-4) | 3.589(-3) | 2.455(-3) | 3.176(-3) | |
(a) Coulomb only (b) Coulomb + Gaunt
To conclude, let us just point out that, contrary to the non relativistic approximation, the multiconfiguration approach is required, in the relativistic case, not only to include correlation effects but also to handle intermediate coupling scheme as soon as open shells are involved.
Acknowledgements
The author is indebted to Dr P. Indelicato for his many contributions to the improvements in the code and especially in the calculation of radiative corrections. The Welton approximation of the screening correction to the self energy belongs to him.
The method we used [33] is unsophisticated in the sense that it did not use any fractional parentage
coefficients but it is easy to implement in a computer code and is quite general. Indeed the only limitation is
the size of the matrix to be diagonalized. We may also note that the same approach has been used in the non
relativistic case [34]. The wavefunction being written as a sum of Slater determinants all of them having the
same 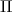 and M values it is easy to calculate the matrix of J2 and then to diagonalize it to obtain the
eigenstates of the total angular momentum (i.e. the coeffiecients di of Eq.(6)). To compute the matrix of J2
first remember that:
and M values it is easy to calculate the matrix of J2 and then to diagonalize it to obtain the
eigenstates of the total angular momentum (i.e. the coeffiecients di of Eq.(6)). To compute the matrix of J2
first remember that:
![J2 = sum j2 + 2 sum sum jA .jB
A A A B<A
sum 2 sum sum [( - + - + ) z z]
= AjA + A B<A jAjB + jBjA + 2jAj B](mettec69x.gif) | (59) |
Then, as the one-electron orbitals are assumed to be orthonormalized, it is enough to compute the
expectation value of J2 between two determinants 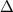 in the three following cases:
in the three following cases:
1) the two determinants are the same
![<D |J2 |D > = sum j (j + 1) + sum sum {2m m - d [j (j + 1)- m m ]}
A A A A B<A A B A,B A A A B](mettec70x.gif) | (60) |
with the short hand notation:
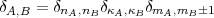 | (61) |
2) the two determinants are different by one orbital (A  A')
A')
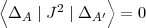 | (62) |
3) the two determinants are different by two orbitals (A  A') and (B
A') and (B  B')
B')
![<DA,A' |J2 |DB,B'> = dA,A'dB,B'{[jA (jA + 1) - mAmA'] [jB (jB + 1) - mBmB']}1/2 -
1/2
dA,B'dB,A'{[jA (jA + 1) - mAmB'] [jB (jB + 1) - mBmA']}](mettec73x.gif) | (63) |
[1] E.E. Salpeter and H.A. Bethe. Phys. Rev., 84, 1232, 1951.
[2] J. Sucher. Phys. Rev., 103, 468, 1956.
[3] A.I. Akhiezer and V.B. Berestetskii. Quantum Electrodynamics. John Whiley & Sons Inc., New York, 1965.
[4] J.P. Desclaux. Comp. Phys. Commun., 9, 31, 1975.
[5] S. Love. Ann. Phys., NY, 113, 153, 1978.
[6] J. Sucher. J. Phys. B: At. Mol. Phys., 21, L585, 1988.
[7] I. Lindgren. J. Phys. B: At. Mol. Phys., 23, 1085, 1990.
[8] J. Hata and I.P. Grant. J. Phys. B: At. Mol. Phys., 17, L107, 1984.
[9] P. Indelicato and J.P. Desclaux. Phys. Scripta, to be published, 1992.
[10] C. Froese-Fischer. The Hartree-Fock Method for Atoms. John Wiley & Sons Inc., New York, 1977.
[11] D.R. Hartree. The Calculations of Atomic Structures. John Wiley, New York, 1957.
[12] F.B. Hildebrand. Introduction to Numerical Analysis. McGraw Hill, New York, 1956.
[13] P.J. Mohr. Phys. Rev. A, 46, 4421, 1992.
[14] N.J. Snyderman. Ann. Phys., NY, 211, 43, 1991.
[15] S.A. Blundell. Phys. Rev. A, 46, 3762, 1992.
[16] P.J. Mohr. Ann. Phys., NY, 88, 26, 1974.
[17] P.J. Mohr. Phys. Rev. A, 26, 2338, 1982.
[18] P.J. Mohr and Y.K. Kim. Phys. Rev. A, 45, 2727, 1992.
[19] E.H. Wichmann and N.M. Kroll. Phys. Rev., 101, 843, 1956.
[20] E.A. Uehling. Phys. Rev., 48, 55, 1935.
[21] G. Kallen and A. Sabry. K. Danske Vidensk. Selsk. Mat.-Fis. Medd., 29, 17, 1955.
[22] J. Blomqvist. Nuc. Phys. B, 48, 95, 1972.
[23] L.W. Fullerton, and G.A. Rinker,Jr. Phys. Rev. A, 13, 1283, 1976.
[24] K.N. Huang. Phys. Rev. A, 14, 1311, 1976.
[25] P.J. Mohr. Phys. Rev. Lett., 34, 1050, 1975.
[26] P. Indelicato, O. Gorceix and J.P. Desclaux. J. Phys. B: At. Mol. Phys., 20, 651, 1988.
[27] T.A. Welton. Phys. Rev., 74, 1157, 1948.
[28] P.K. Kabir and E.E. Salpeter. Phys. Rev., 108, 1256, 1957.
[29] R. De Serio, H.G. Berry, R.L. Brooks, J. Hardis, A.E. Livingston and S.J. Hinterlong. Phys. Rev. A, 24, 1872, 1981.
[30] W.R. Johnson and G. Soff. At. Dat. Nuc. Dat. Tables, 33, 405, 1985.
[31] D.F. Mayers. J. de Physique, 11-12, C4-221, 1970.
[32] J.P. Desclaux, C.M. Moser and G. Verhaegen. J. Phys. B: At. Mol. Phys., 4, 296, 1971.
[33] G. Bessis N. Bessis and J.P. Desclaux. J. de Physique, 11-12, C4-231, 1970.
[34] W. Eissner and H. Nussbaumer. J. Phys. B: At. Mol. Phys., 2, 1028, 1969.